7章 プログラム検査を論理で考える

7.1 プログラムの意味

7.1.1 Floyd/Hoareの方法

(1) Hoareの3つ組み

プログラムを論理で表す

P.165下～

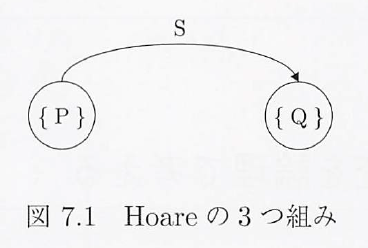
{事前条件}実行文{事後条件}

P.166中～

While言語: 代入/逐次/分岐/繰り返し

(2) 公理的な意味

代入文

Q[E/x] ＝ Qの中に出てくるxにEを代入した命題

{3>0}x:=1+2{x>0}

逐次実行

{P}y:=3;x:=y-2{x>0}
{P}y:=3{R} {R}x:=y-2{x>0}
∴R=y>2
{P}y:=3{y>2}
∴P=3>2

条件分岐文

繰り返し文

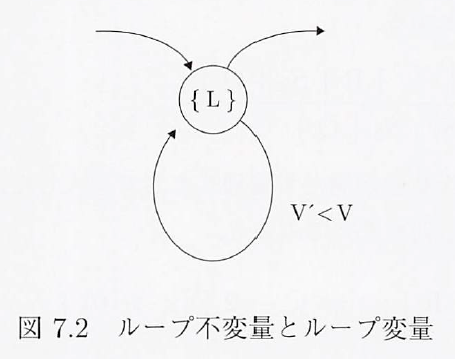
ループ不変量 はCをながめて見つけないといけない

P.168下～

終了判定条件≠whileの条件

終了する＝ループ変量が有界

帰結規測

プログラムに直接関係ない、命題の言い換え

{x=0}x:=x+1{Q=(x=1)}

Q⇒Q'

{x=0}x:=x+1{Q'=(x>0)}

P.169上～

不変量と他の間をつなぐ

[ex12-1] 次のときPはどれですか：{P}x:=1{x>0}

[ex12-2] 次のときPはどれですか：{P}x:=y-1{x>0}

[ex12-3] 事後条件がx>2とすると、if x<2 then x:=3 else y:=3 の事前条件はどのようになりますか

7.1.2 プログラムの振る舞い解析の例

(1) 証明条件の作成

事前/事後条件が1階論理

→ 規則表現するには高階論理が必要

P.170上～

… ← 事前条件 ← 事後条件

P.170中～

Q: 行番号3

P.170中～

if2: 行番号3+2

P.170下～

asgn1: 行番号3+2+1

P.170下～

(2) 繰り返し文のあるプログラム

不変量として x >= y を採用

P.171中～

Q: 文番号3

P.171下～

ichi: 文番号2後+3+帰結規則

P.171下～

ni: 文番号2前+帰結規則

asgn2: 文番号2文

P.172上～

wh2=iv

asgn1: 文番号1

P.172中～

事後→事前と1つながってないので3つ必要

P.172中～

無条件には成り立たないが、x>=0ならOK

[ex12-4] if (x==0) then y:=x else y:=1 とその事後条件Qを表すものはどれですか

[ex12-5] while(y!=x) do y:=y+1 end の不変量となりえないものはどれですか

教科書（図はすべてこちらより引用）：
　中島震，「形式手法入門―ロジックによるソフトウェア設計―」，オーム社