


省略
iterate: 複数のオブジェクトにある操作を行う
P.114下~
existsやforAllもiterateを使って表す & iterateは有限にしか使えない
⇒ 論理記述が厳密にはできない
ナビゲーション: あるクラスと関連のあるオブジェクトを洗い出す
P.116上~
未定義≠空集合
P.116上~
あるクラスについてのシステム状態:
- そのクラスのオブジェクトの集合
- オブジェクトのプロパティの集合
- 他のクラスへのリンクの集合
P.117下~
オペレーション(メソッド)を、事前状態と事後状態で表す。
P.118上~
不変量はforAllで表すことが多いが、前述のように無限を対象にはできない
[ex9-1] forAllの対象が有限集合に限定され、無限集合には使えないのはどちらの扱いをしているときですか
[ex9-2] 検証結果が厳密に論理に従っているといえるのはどの場合ですか

subp関数(5,3)
= 1+subp関数(5,4) = 1+(1+subp関数(5,5)) = 1+(1+0) = 2
→ subp関数はsubp仕様を満たしそう
P.119上~
P.119中~
subp関数(0,1) = 1+subp関(0,2) = 1+(1+subp関数(0,3)) : (値が返ってこない)
これはsubp仕様を満たしているといえるのか?
部分関数:定義域の一部に対してしか値が返ってこない関数
P.119下~
“未定義値”を返すという考え方がある
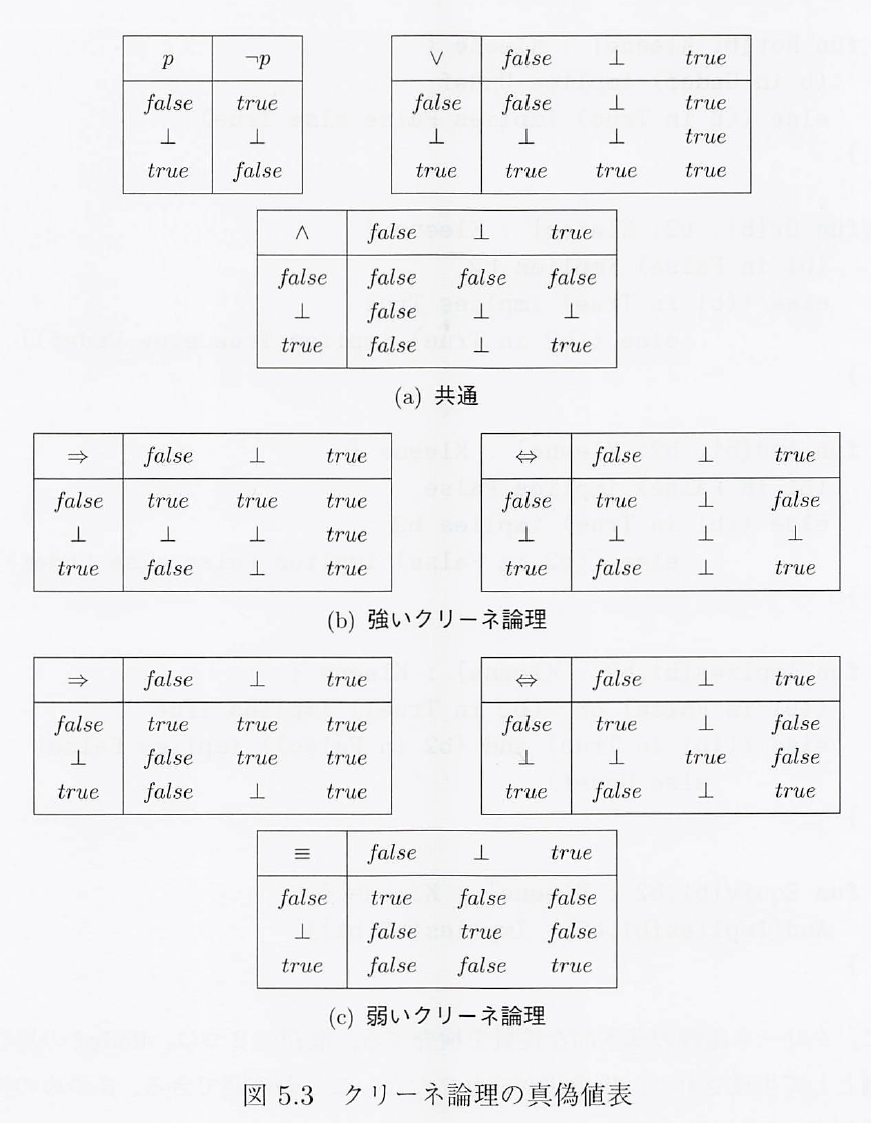
true / false / ⊥(bottom)
P.120下~
⊥⇒⊥ = ⊥ : ⊥から新たなものは生まれないという解釈
⊥⇒⊥ = true : ⊥という一の値があるという解釈
P.121下~
省略
[ex9-3] 論理値としてtrue/falseに加えて⊥を考える必要性はどの辺りにありますか
[ex9-4] 強いクリーネ代数でも弱いクリーネ代数でもあり得ないのはどれですか

教科書(図はすべてこちらより引用):
中島震,「形式手法入門―ロジックによるソフトウェア設計―」,オーム社