2S-ALH @2017/06/28 “線型代数 中間試験範囲の復習”

ベクトルの内積

試験問題[8](2) 1辺の長さが \(2\) の正四面体 \(OABC\) について，\(\vec{OA}\perp\vec{BC}\) を証明せよ．

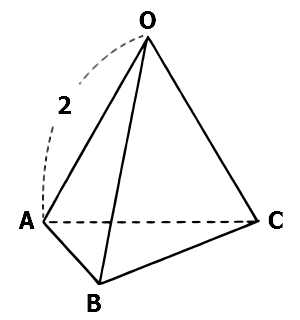
垂直を示すにはどうしたらよいか見当がつかない場合

• \(\vec{OA}\) と \(\vec{BC}\) の間の角 \(\theta\) の話をしたい
• だが問題には正四面体（つまり全部 \(60^\circ\) ）ということしか出てきていない
• 間の角 \(\theta\) が必要なので，何か \(\cos\theta\) が出てくる話を習ったことを思い出す
• たしか内積 \(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cdot\cos\theta\) だった
• 角 \(\theta\) を導くために内積 \(\vec{OA}\cdot\vec{BC}\) を考える（下に続く）

垂直→内積ゼロ がピンときた場合

\(\vec{OA}\cdot\vec{BC}\)
\(=\vec{OA}\cdot(\vec{OC}-\vec{OB})\)
\(=\vec{OA}\cdot\vec{OC}-\vec{OA}\cdot\vec{OB}\)
\(=|\vec{OA}||\vec{OC}|\cos 60^\circ - |\vec{OA}||\vec{OB}|\cos 60^\circ\)
\(=2\cdot2\cdot\frac{1}{2}-2\cdot2\cdot\frac{1}{2}\)
\(=0\)

（つまり，\(|\vec{OA}||\vec{BC}|\cos\theta=0\)）
（よって，\(\cos\theta=0\)．∴ \(\theta=90^\circ\)）
∴ \(\vec{OA}\perp\vec{BC}\)

平面の方程式

試験問題[10] 3点 \(A(1,1,-1), B(0,1,3), C(4,3,1)\) を通る平面の方程式を求めよ。

\(\vec{AB}=(-1,0,4)\)，\(\vec{AC}=(3,2,2)\)

方法1： 法線ベクトルを使う（＝模範回答）

法線ベクトル \((a,b,c)\) で定まり \((x_0,y_0,z_0)\) を通る平面の方程式は，
\(a(x-x_0)+b(y-y_0)+c(z-z_0)=0\)

求める平面の法線ベクトルを \(\vec{n}=(a,b,c)\) とすると，
\(\vec{n}\perp\vec{AB}\) より，\(-a+4c=0\) …(1)
\(\vec{n}\perp\vec{AC}\) より，\(3a+2b+2c=0\) …(2)
(1)より \(a=4c\)，さらに(2)より \(b=-7c\) ．
よって，
\(4c(x-1)-7c(y-1)+c(z+1)=0\)
\(c\) で割って，
\(4x-7y+z+4=0\)

方法2： ベクトルの和で表す

求める平面は，
\((x,y,z)\)
\(=\vec{OA}+u\vec{AB}+v\vec{AC}\)
\(=(1,1,1)+u(-1,0,4)+v(3,2,2)\)
よって，
\[\begin{eqnarray} \left\{ \begin{array}{l} x=1-u+3v\\ y=1 +2v\\ z=-1+4u+2v \end{array} \right. \end{eqnarray}\]

これから \(u,v\) を除去すると，
\(4x-7y+z+4=0\)

直線の方程式

試験問題[11] 次の2直線は交わるか．交わるときは，その交点の座標を求めよ．
　\(x-1=\frac{y+1}{2}=\frac{z+5}{2}\) …(1)
　\(\frac{x-6}{2}=\frac{y+1}{-1}=\frac{z-1}{2}\) …(2)

（模範回答では \(s,t\) とおいていたが…）
\(2x-2=y+1=z+5\) …(1')
\(x-6=-2y-2=z-1\) …(2')
(1')-(2')
\(x+4=3y+3=6\)
これより \(x=2\)，\(y=1\) ，
最後に \(z=-3\) も得られる．
これら \(x,y,z\) は(1),(2)を満たす．
∴ \((2,1,-3)\) で交わる．

　
　
　

---

この資料はwebで公開しています：

西村のオフィシャルサイト（「大分高専 西村」で検索）→ 一番下のリンク → 授業 → 2S ALH