2S-ALH @2017/06/07 “平面のベクトル”
ベクトルの演算
\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\), \((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\)
\(m(n\vec{a})=(mn)\vec{a}\), \((m+n)\vec{a}=m\vec{a}+n\vec{a}\), \(m(\vec{a}+\vec{b})=m\vec{a}+m\vec{b}\)
問題A. 下のベクトル \(\vec{PQ}\) を \(\vec{a},\vec{b},\vec{c},\vec{d}\) で表せ.
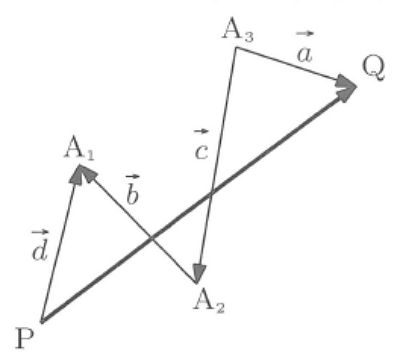
問題B. \(3(-\vec{a}+4\vec{b})+2(2\vec{a}-5\vec{b})\) を簡単にせよ.
問題C. \(2\vec{a}+(\vec{b}-\vec{x})=-3\vec{x}-\vec{a}+3\vec{b}\) のとき,\(\vec{x}\) を \(\vec{a}, \vec{b}\) で表せ.
問題D. \(|\vec{a}|=5\) のとき,\(\vec{a}\) と向きが反対で大きさが \(1\) のベクトルを求めよ.
ベクトルの成分
\(A(a_1,a_2),B(b_1,b_2)\) ⇒ \(\vec{AB}=(b_1-a_1,b_2-a_2)\)
\(\vec{a}=(a_1,a_2)\) ⇒ \(|\vec{a}|=\sqrt{a_1^2+a_2^2}\)
問題A. \(\vec{a}=(-2,3)\),\(\vec{b}=(1,-1)\) のとき,\(2\vec{a}-\vec{b}\) の大きさを求めよ.
問題B. \(\vec{a}=(-2,3)\),\(\vec{b}=(1,-1)\) のとき,\(\frac{1}{2}\vec{a}+\vec{b}\) の大きさを求めよ.
問題C. \(A(1,-1)\),\(B(3,1)\) のとき,\(\vec{AB}\) の大きさを求めよ.
問題D. 3点 \(A(-1,0), B(2,-1), C(x,y)\) と正の実数 \(k\) について,\(\vec{AC}=k\vec{AB}\),\(|\vec{AB}|=20\) が成り立つとき,\(k\) の値を求めよ.
ベクトルの内積
\(\vec{a}\cdot\vec{b}\) \(=|\vec{a}||\vec{b}|\cos\theta\) \(=a_1b_1+a_2b_2\)
問題A. \(|\vec{a}|=4, |\vec{b}|=2, \theta=\frac{\pi}{6}\) のとき,\(\vec{a}\) と \(\vec{b}\) の内積を求めよ.
問題B. \(|\vec{a}|=2, |\vec{b}|=\sqrt{3}, \theta=\frac{3}{4}\pi\) のとき,\(\vec{a}\) と \(\vec{b}\) の内積を求めよ.
問題C. \(\vec{a}=(1,-3)\) と \(\vec{b}=(-2,-1)\) の内積を求めよ.
問題D. \(|\vec{a}|=\sqrt{3}, |\vec{b}|=\sqrt{5}, \vec{a}\cdot\vec{b}=1\) のとき,\((2\vec{a}-\vec{b})\cdot(\vec{a}+\vec{b})\) を求めよ.
ベクトルの平行と垂直
\(\vec{a}\parallel\vec{b} \Leftrightarrow \vec{b}=m\vec{a}\) を満たす \(m\) が存在
\(\vec{a}\perp\vec{b} \Leftrightarrow \vec{a}\cdot\vec{b}=0\)
\((\vec{a}\ne0, \vec{b}\ne0)\)
問題A. \(\vec{a}=(2,k)\) と \(\vec{b}=(-3,k+5)\) が平行となるように \(k\) の値を定めよ.
問題B. \(\vec{a}=(1,3)\) と \(\vec{b}=(k,k+4)\) が平行となるように \(k\) の値を定めよ.
問題C. \(\vec{a}=(2,-1)\) と \(\vec{b}=(k-1,k)\) が垂直となるように定数 \(k\) の値を定めよ.
この資料と解答はwebで公開しています:

情報工学科のサイト(「大分高専 情報」で検索)→ スタッフ紹介(教職員紹介) → 西村俊二 → 一番下のリンク → 2S ALH
解説及び問題は下記より:
高遠節夫他,「新線型代数問題集」,大日本図書